Exploring tensor products
Date:
Introductory talk organized by the Stellenbosch University Mathematics Society (SUMS) for an undergraduate audience.
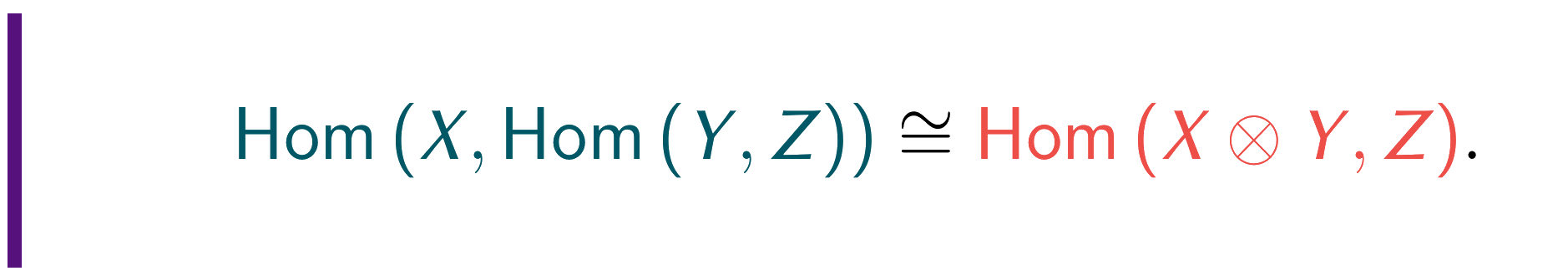
Overview
In this talk, we take a tour through a number of increasingly abstract definitions for tensors and the tensor product, starting at the component-wise definition in terms of transformation properties which is common in physics literature, and working towards category-theoretic definitions and the tensor-hom adjunction.
The goal of this talk is a pedagogical one: I wish to exhibit tensors in their full basis-free and abstract generality, but also connect this to the concrete incarnation used by physicists. This is motivated by my own past frustration at having had need for tensors in physics well before encountering rigorous definitions.
Notable inclusions & omissions
The time constraint and level of the audience force me to make some concessions; the most egregious of which is that I do not actually define categories or adjunctions, but merely borrow some terminology from category theory. I also begin by defining vector spaces, since some first-years in attendance will not have seen the abstract definition.
Another notable omission is a discussion of tensor algebras, (anti)symmetrization, and similar further topics in multilinear algebra.
