Junior lecturer

In the first half of 2024, I lectured first year mathematics at Stellenbosch University, covering mainly precalculus and calculus. I taught a class of approximately 220 students.

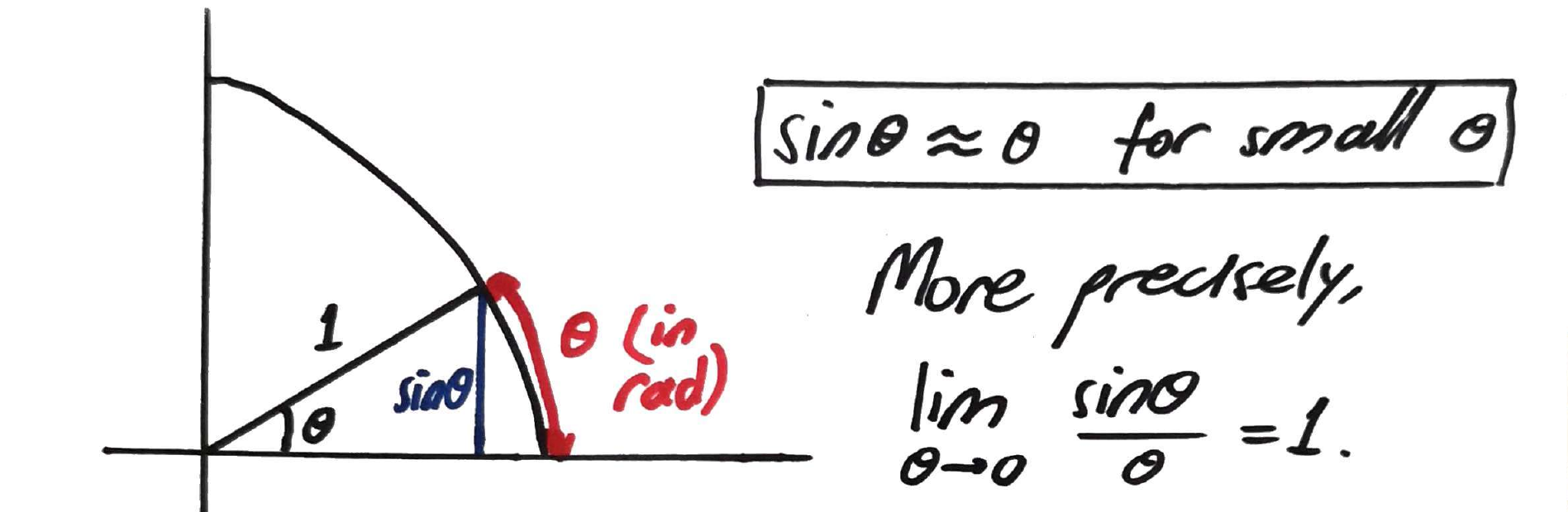
My duties

• Teaching classes (5h of lectures each week)
• Compiling tutorials & memoranda
• Compiling & marking exams
• Corresponding & meeting with students as needed

Student feedback

ROCTAS (Recognition of Contributions Towards Academic Success) Award (May 2025)
Passing students from the 2024 freshman cohort were invited to nominate (with motivation) the single lecturer who contributed most towards their academic success.

I set up an anonymous feedback system for my classes whereby students could review my lectures and submit comments. My feedback was generally positive, with the main criticisms usually pertaining to the pace of the curriculum, my vocabulary being inaccessible, or my tendency to speak quickly. Several students expressed appreciation of my enthusiasm toward the subject. Some comments along these lines are given below (selected with some obvious bias):

Love the Lectures, I never liked math in High school but your enthusiasm and knowledge make this module enjoyable.

I appreciate your style of lecturing. Your focus on developing a deeper understanding of the concepts reflects what I believe to be the benefit of an academic university environment.

Overall your class is interesting and you make maths (that is a headache for some) to be fun! Your intelligence is inspiring and your excitement about the subject is refreshing.

I really enjoy your enthusiasm for math, it is highly contagious. Thank you for your positivity.

My mathematics lecture is what I look forward to quite often in the week. It is a conducive and learning friendly environment. My lecturer’s passion is what inspires me to be as passionate about mathematics.